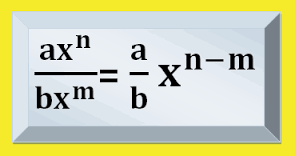Álgebra es el nombre que identifica a una rama de las matemáticas que emplea números, letras y signos para referenciar a múltiples operaciones aritméticas. El término viene del vocablo árabe que significa "reducción"

Hoy entendemos como álgebra al área matemática que se centra en las relaciones, estructuras y cantidades. La disciplina que se conoce como álgebra elemental, en este marco, sirve para llevar a cabo operaciones aritméticas (suma, resta, multiplicación, división) pero que, a diferencia de la aritmética, se vale de símbolos (a, x, y) en lugar de utilizar números. Esto permite formular leyes generales y hacer referencia a números desconocidos (incógnitas), lo que posibilita el desarrollo de ecuaciones y el análisis correspondiente a su resolución. Veamos como se aplica el álgebra al campo de las matemáticas...

Una expresión algebraica es un conjunto de cantidades numéricas y literales relacionadas entre sí­ por los signos de las operaciones aritméticas como sumas, diferencias, multiplicaciones, divisiones, potencias y extracción de raí­ces.

Si x es una variable, entonces un monomio en x es una expresión de la forma axⁿ, en donde a es un número real y n es un entero no negativo.   Un binomio es la suma de dos monomios que no se pueden simplificar y un trinomio es la suma de tres monomios que no se pueden simplificar.

Recuerda siempre que un monomio tiene solo un término, un binomio dos términos y un trinomio tres términos.

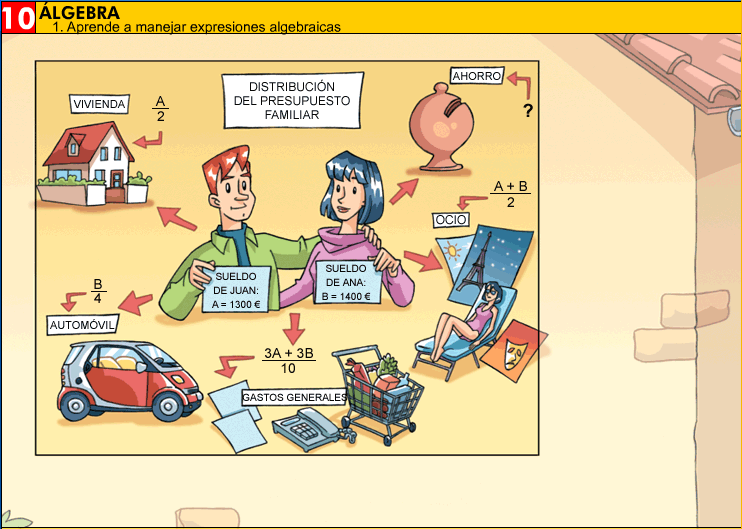
Las expresiones algebraicas surgen al traducir al lenguaje matemático situaciones en las que aparecen datos desconocidos que se representan con letras.

Las expresiones algebraicas más sencillas formadas por productos de letras y números se llaman  monomios.

Un monomio consiste en el producto  de un  numero conocido (coeficiente) por una o varias letras (parte literal)

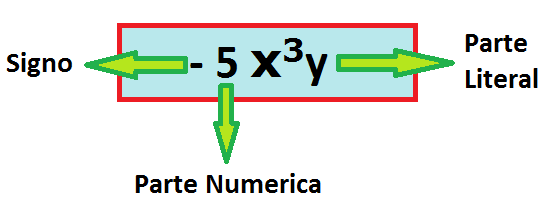
El  grado  de una letra es el exponente al que está elevada. Se llama  grado de un monomio  a la suma de los grados de las letras que lo forman

Monomios semejantes  son los que tienen la misma parte literal (las mismas letras con los mismos exponentes).

SUMA Y RESTA DE MONOMIOS 

Los monomios sólo se pueden sumar (o restar) cuando son semejantes, es decir cuando tienen la  misma parte literal.

Cuando no son semejantes la operación se deja indicada.

Fíjate en cómo se resuelven los siguiente ejemplos

MULTIPLICACIÓN DE MONOMIOS

Un monomio es un producto. Por lo tanto al multiplicar  dos monomios  obtenemos un producto con más factores, es decir otro monomio

Como puedes comprobar el producto de dos monomios es siempre otro monomio.

Fíjate, podemos obtener directamente el resultado si se multiplican primero los coeficientes y luego la parte literal (recuerda que  para  multiplicar potencias de la misma base se deja la base común y se suman los exponentes).

MULTIPLICACIÓN DE UN MONOMIO POR UNA SUMA O RESTA

Cuando uno de los factores es una suma, aplicamos la propiedad distributiva a (b + c) = ab + ac, es decir multiplicamos el factor por cada uno de los sumandos que forman el otro factor.   

DIVISIÓN DE MONOMIOS

Para dividir monomios  seguimos aplicando lo que sabemos sobre operaciones  con números  sin necesidad de aprender procedimientos nuevos.

Para proceder correctamente primero dividimos los coeficientes, después se divide las partes literales teniendo en cuenta que para dividir potencias e la misma base se restan los exponentes.