Trabajemos con geometría
Área del circulo
En este apartado, trabajaremos una temática relacionada con el área de una circunferencia y un circulo, sin embargo antes de abordar dichos temas es necesario recordar algunos conceptos básicos… te invito a que mires los videos y realices las actividades propuestas.

Hoy en clase de matemáticas, el profesor nos dijo que un circulo es diferente a la circunferencia.....
¿RECUERDAS CÚAL ES LA DIFERENCIA?

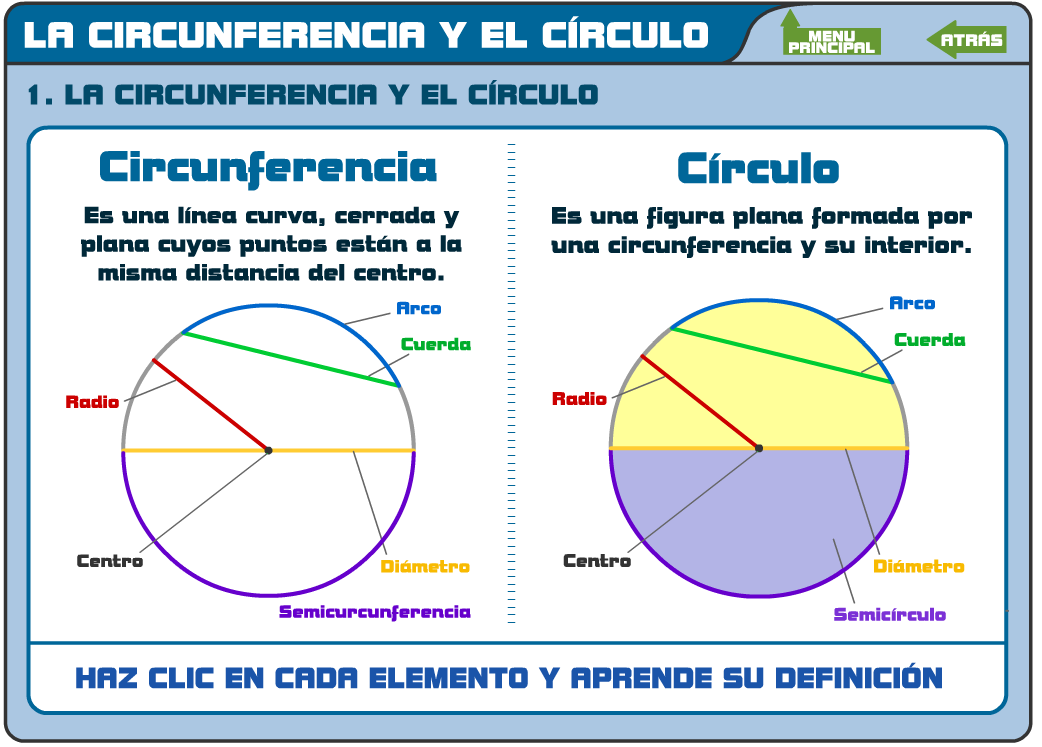
CIRCUNFERENCIA Y CIRCULO
Circunferencia es el conjunto de todos los puntos del plano que equidistan de un mismo punto llamado centro de la circunferencia. El punto centro no pertenece a la circunferencia. La circunferencia se nombra con la letra del centro y un radio.
Círculo es la figura plana formada por una circunferencia más toda su región o área interior
Ejemplos prácticos de una circunferencia : Aro, anillo, hula-hula, borde de un vaso, la orilla de un plato, etc.



ÁREA DEL CIRCULO
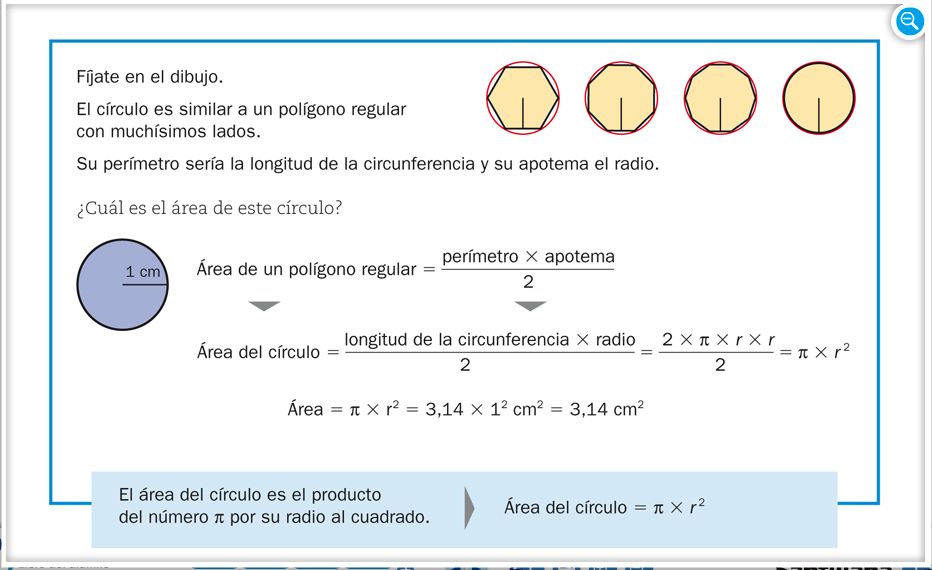
Área del círculo
¿De dónde sale la fórmula?
Si buscamos en los libros encontramos que el área del círculo se calcula usando la fórmula:
A = π x r²
Pero, ¿de dónde viene esta fórmula?
Lo que vamos a hacer es romper un círculo en pequeños trozos y con ellos volver a armarlo en una forma de la cual conocemos cómo calcular su área... el rectángulo.
Tal vez te preguntes ¿cómo haremos para reordenar las piezas de un círculo y armar un rectánculo? Vamos a verlo... ¡es fácil!
Comenzaremos con el círculo que queremos dividir:

Ahora dividiremos el círculo en 4 partes iguales:




Luego las ensamblamos tratando de formar un rectángulo:

No es exactamente un rectángulo, ¿no?. Pero no hemos terminado todavía.
Vamos a romper el círculo en trozos más pequeños, en octavos:








... y organizamos las piezas en forma rectangular:
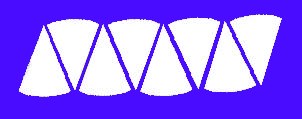
Este sin duda comienza a verse como un rectángulo, ¡pero todavía falta!. El siguiente paso es volver a dividir en trozos más pequeños:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Al ponerlos juntos estamos más cerca de parecerse a un rectángulo:

El objetivo es lograr una forma lo más cercana posible al rectángulo, de manera que podamos encontrar su área utilizando la fórmula del rectángulo: A = l x a
Seguimos rompiendo el círculo en piezas más pequeñas. Al ordenar todas las piezas, la forma sería algo como esto:

Esta figura es muy cercana a un rectángulo perfecto, pero puedes ver que la parte superior e inferior no están aún perfectamente rectas.
¿Puedes visualizar lo que sucederá si continuamos rompiendo el círculo en piezas cada vez más y más pequeñas?
Las piezas serían tan pequeñas que no las podríamos ver, y la parte superior e inferior del rectángulo formado con ellas, parecería perfectamente recta. Esto es lo que queremos ver:

¡Un rectánculo perfecto!. Ahora todo lo que tenemos que hacer es encontrar su área, utilizando la fórmula A = l x a

La siguiente pregunta es: ¿Cuál es el largo y el ancho de nuestro rectángulo hecho con partes del círculo?
Vamos a volver a una imagen anterior, para que puedas ver las partes del círculo más claramente:

La longitud del círculo original es la distancia alrededor, o sea la circunferencia:
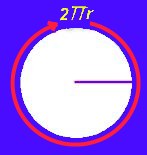
La mitad de esta distancia alrededor del círculo, πr, va en la parte superior del "rectángulo", y la otra mitad, también de longitud πr, va en la parte inferior:

En otras palabras, sumadas la parte superior e inferior obtenemos 2πr, o sea la longitud de la circunferencia.
El ancho del "rectángulo" es el radio del círculo r.
Entonces, sabemos que el largo del "rectángulo" es πr y el ancho es r. Ahora podemos encontrar el área del rectángulo formado con pequeños trocitos del círculo, usando la fórmula del rectángulo:
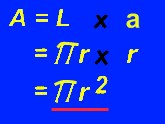
... y allí tenemos la fórmula para el área del círculo con la cual comenzamos!